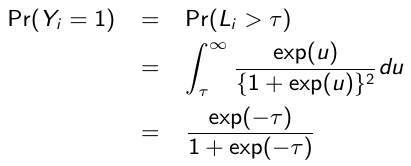Features of GLM and Marginal Methods

In many biomedical applications outcomes are binary, ordinal or a count. In such cases we consider extension of generalized linear models for analyzing discrete longitudinal data. These non-linear models require that a linear transformation of the mean response can be modeled in a regression setting. The non-linearity raises issues with the interpretation of the regression coefficients.

We let Y_i denote the response variable for the i^th subject, and: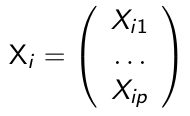

is a p*1 vector of covariates. A generalized linear model for for Y_i  needs the following three-part specification:

1. A Distributional Assumption

Generalized linear models assume that the response variable has a probability distribution belonging to the exponential family (normal, bernoulli, binomial or Poisson). A feature of the exponential family is the variance can be expressed as:

Where phi is a dispersion parameter and v(μ_i) is the variance function. For example:

• Variance function of normal distribution: v(μ) = 1
• Variance function of Bernoulli: v(μ) = μ(1 - μ)

2. A Link Function

The link function g(.) applies to the mean and then links the covariates to the transformed mean η such that:

For example, the canonical link functions for some common distributions are: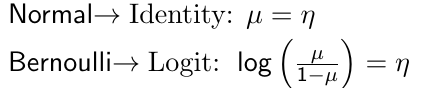

3. A Systematic Component

The systematic component specifies the effects of the covariates X_i on the mean of Y_i can be expressed in terms of the following linear predictor:

Note that the term 'linear' refers to the regression parameters.

Binary response

Let Y_i denote a binary response variable with two categories such as presence or absence of a disease. The probability distribution is Bernoulli with Pr(Y_i = 1) = μ_i and Pr(Y_i = 0) = (1 - μ_i). Using the logit as the link function we have:

Where μi / (1 - μi) are the odds of success

A unit change of X_ik changes the odds of success multiplicitively by a factor of exp(β_k).

The logistic regression model can be derived from the notion of a latent variable model. Suppose that L_i is a latent continuous variable which follows a standard logistic distribution (0,  π²/3) and that a positive response is observed only when Li exceeds some threshold  τ , such that:

It can be shown that: