Linear Mixed Effects Modeling

The simplest mixed effect model is a random intercept model where Z_i = 1;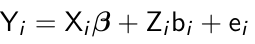

The random intercept model can be interpreted as the effect of all unobserved subject-specific variables (b_i) on the linear predictor.

Random slopes of time-varying covariates (Z_i) can be interpreted as interaction of unobserved subject specific covariates with observed time-varying covariates.

We can also include a random effect with a time-invariate covariate z_i (e.g. treatment group) to produce a heteroscediastic random intercept b_i0 + b_i1z_i.

Two-Stage Formulation

An alternative formulation of the mixed effects models is a two-stage formulation, in which we first specify a within subject or level-1 model where the occasion specific linear predictor is a function of time-varying covariates. Then a between subject or level 2 model is specified: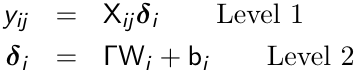

Some elements of δ_i are constant and some depend only on the observed covariates.

Consider the following with a random intercept and a random slope for time: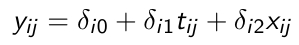

x_ij is a time-varying covariate and w_i is a time-invariant covariate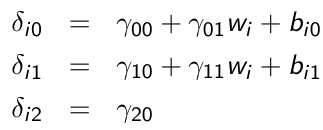
The redirected form is obtained by substituting the level-2 model into level-1 model. We then substitute level-2 into level-1 to produce the reduced form with a "cross-level interaction" term γ₁₁w_it_ij

• The two formulations are equivalent but it can have an impact on the types of models being considered
• The two-stage formulation encourages inclusion of many cross-level interactions and few same-level interactions
• Due to an abundance of interactions in the two-stage formulation, we usually center around the mean all variables except time. In our example, centering of w_i makes γ₁₀ interpretable as the mean effect of t_ij when t_ij when w_i takes it mean value.