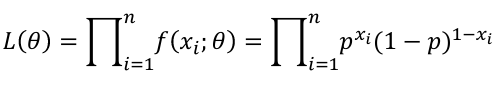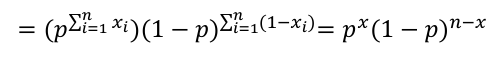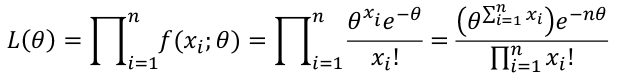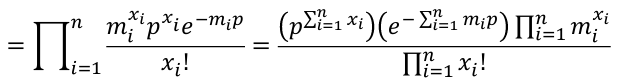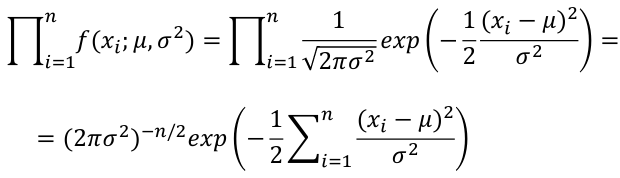Module 6 & 7: Summary Statistics and Parameter Estimation

Since it is practically impossible to enroll the whole target population, we take a sample - a subgroup representative of the population. Since we're not examining the whole population, inferences will not be certain. Probability is the ideal tool to model and communicate uncertainty inherent with informing the population characteristic based on a sample. Inferences are categorized into two broad categories:

1. Estimation - Estimate the value of a parameter based on a sample
2. Hypothesis Testing - Comparing parameters fir two sub-populations using tests of significance

For smaller sample sizes (n < 30) we can use a t distribution.

Parameter Estimation

In many statistical problems we make an assumption on the probability distribution from which the data are generated. Maximum likelihood is an approach based on selecting the parameter values that make the observed sample most likely.

If X_i, ... X_n is a sample of independent observations from X~f(x; 𝜃), the likelihood function is defined as:

The product of each observation (marginals); As a joined distribution is the product of the marginals when the observations are independent (identically distributed). For binomial distributions, this can be further simplified:

For a Poisson Likelihood with the mean -> p(X=x) = (𝜃^x_i*e^-𝜃)/x!; 𝜃 = mean

We could also express the Poisson likelihood function in terms of rates for each subject. So X_i ~ Poisson(m_i*p); where m is the number of trials and p is the probability of success, and assuming independence.

For a Normal Distribution likelihood can be expressed in terms of mean and variance:

MLE

The Maximum Likelihood Estimate (MLE) is the value of the parameter that maximizes the likelihood equation. Often we work with the log-likelihood because it will lead to the same maximime (since log is a strictly increasing function). To find this with calculus  we can differentiate and set the derivative to 0.

For Binomial:

L(p) = p^x(1-p)^n-x

l(p) = log(L(p)) = x*log(p) + (n-x)*log(1-p)

dl(p) / dp = x / p - (n-x) / (1 - p) = 0

(x*(1 - p) - (n-x)*(1 - p)) / (p*(1 - p) = 0

x = np -> p_hat=x/n

Based on CLT, when n is large:

X ~ N(np, np(1-p)) and p_hat = x / n ~ N(p, p(1-p)/n)