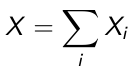Module 4: Discrete Distributions

For any domain there are infinitely many distributions. The most common and famous distributions get a name; Binomial, Negative Binomial, Geometric, Hypergeometric, Poisson, etc. In this section we focus on Binomial and Poisson distributions.

The Bernoulli Distribution is a special member of the distribution family. It is the simplest example of a Binomial distribution, with only two domains (aka dicothomous distribution). A experiment which only has two domains is called a Bernoulli experiment. Ex. the number of students who get an A on a test, whether a person has a disease or not.

If we have two Bernoulli independent trials with equal probability of a positive result, we'll refer to that probability as pi

X₁ = { 1 if outcome +, 0 if outcome - }            and              X₂ = { 1 if outcome +, 0 if outcome - }

Then, X = X₁ + X₂

The variable X above is a random variable with domain of {0, 1, 2} as it is a result of the two trials. The distribution is an example of a Binomial (2, pi) distribution.

More generally, if X_i are n Bernoulli independent trials with probability of a positive result equals pi

The domain of X a Binomial (n, pi) is {0, 1, 2... n}. When n=1 the binomial reduces to Bernoulli