| Exposed | Unexposed | ||
| Diseased | a | b | m1 |
| Not Diseased | c | d | m0 |
| n1 | n0 | n |
The LMP is used to specify the priors and the likelihood The GMP is used to generate the conditional distributions to run the Gibbs Sampling
#### Bayesian Hypothesis Testing: Prior Odds On each hypothesis we have a prior probability: P(H0) = P(M0) and P(Ha) = P(M1) Use the data to compute the posterior probability of each hypothesis: [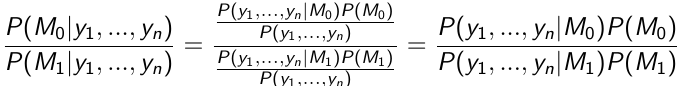](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-01/cd5image.png) This equates to: Posterior ODDs = Bayes Factor \* Prior Odds We accept the hypothesis with maximum posterior probability (0 - 1 loss) The Bayes Factor is the ratio of the likelihood functions computed for models M0 and M1 If P(M0) = P(M1) then the posterior probability of M1 is larger than the posterior probability of M0 We can also assign weights to adjust the probability of making errors: [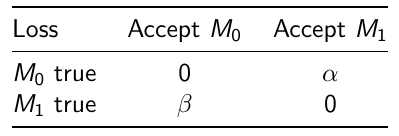](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/image.png) Where alpha would be the loss incurred if M1 is accepted when M0 is true and beta is the loss incurred if M0 is accepted when M1 is true. # Bayesian Linear Regression By now we know what a linear regression looks like. Let's consider a special case where number of parameters, p = 0: [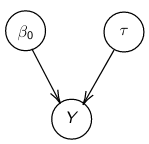](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/4jbimage.png) Assume Y is distributed as a normal distribution with mean β0: Y|β0, τ ∼ N(β0, σ2 = 1/τ )τ = 1 / σ2 , also called **precision** <- Be aware this will be used interchangeably with variance
The density function is: [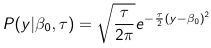](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/ByOimage.png) Mean and variance: E(Y) = μ0; V(Y) = 1/τ0 + τ The Posterior Distribution for β0 is calculated using Bayes' Theorem[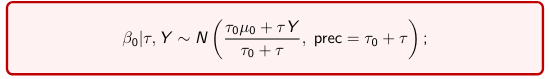](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/lLKimage.png) ##### When Mean and Variance are Unknown We use a Normal prior distribution for the mean β0 ∼ N(μ0, τ0) and a **Gamma** prior distribution for the precision parameter: [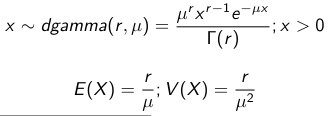](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/0Drimage.png) JAGS example: ``` model.1 <- "model { for (i in 1:N) { hbf[i] ~ dnorm(b.0,tau.t) } ## prior on precision parameters tau.t ~ dgamma(1,1); ### prior on mean given precision mu.0 <- 5 tau.0 <- 0.44 b.0 ~ dnorm(mu.0, tau.0); ### prediction hbf.new ~ dnorm(b.0,tau.t) pred <- step(hbf.new-20) # hbf >= 20 }" ``` #### Predictive Distributions Given the Prior and Observed data we can compute the probability of a new observation will be greater or less than some integer threshold. The predictive distribution is a distribution of unobserved y~, that is: [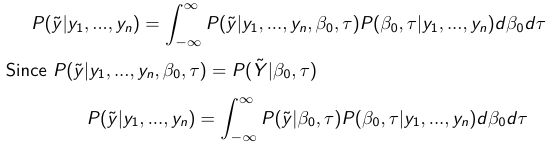](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/7xDimage.png) The two sources of variability in prediction are in the parameters V(β0, τ | y) and the variability in the new observation V(y | β0, τ) - To simulate from predictive density, do repeatedly: 1. Sample one sample β0\*, τ\* from posterior β0, τ | y 2. Sample one y~ ~ N(β0\*, 1/τ\* ) - During the Gibbs sampling we generate samples values from the posterior distribution β0, τ | y - So Generating y~ ~ N(β0, τ | y) will produce the correct predictive distribution samples. P(y~ > 20 | data) is the proportion of y~ > 20 #### Log Normal Distributions Since in the example above the outcome distribution can only be positive we can use a Log-Normal distribution, a continuous distribution with support for values y > 0. [](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/vEWimage.png) Y | η, σ2 ~ INormal(η, σ2) with density function: [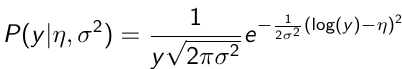](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/ye6image.png) [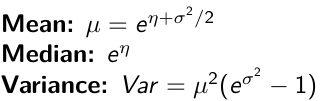](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/NX5image.png) It also implies: Log( Y )~ Normal(η, σ2) In JAGS we use: dlnorm(η, σ2) ``` "model { for (i in 1:N) { hbf[i] ~ dlnorm(lb.0,tau.t) } ## prior on precision parameters tau.t ~ dgamma(1,1); ### prior on mean lb.0 ~ dnorm(1.6,1.6); b.0 <- exp(lb.0) ### prediction hbf.new ~ dlnorm(lb.0,tau.t) pred <- step(hbf.new-20) }" ``` In the above example, we get the initial prior on β0 from previous data, where we derived median(b.0)=5 and V(b.0)=1/0.44=2.27 Then we take the log of the median to get η and transform the precision variable with: log(1 + V (b.0)/E (b.0)2 ), then take the inverse of that to get the variance. #### Parameter Interpretation Let's consider data of the SNP rs766432 on the effect of HbF [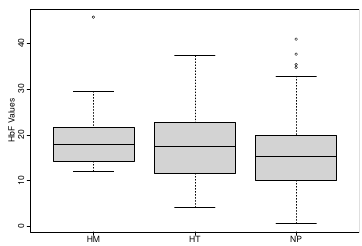](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/edaimage.png) Where HT is heterzygote, HM is homozygoute and NP is common alleles. [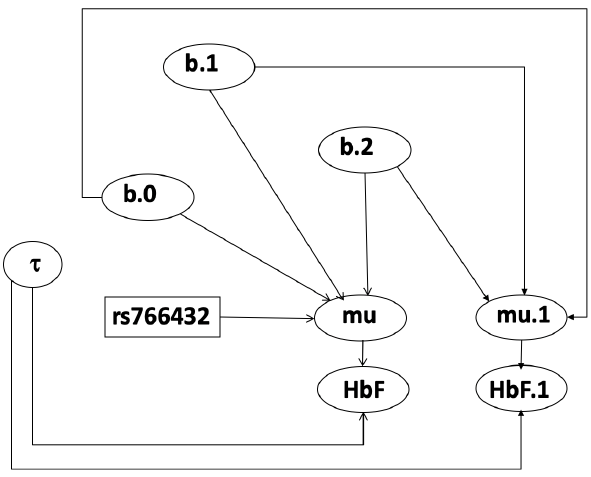](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/HRIimage.png) - We start by creating indicators for HT and NP using the equals( , ) function in JAGS [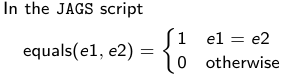](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/iVLimage.png) - The mean of Log HbF [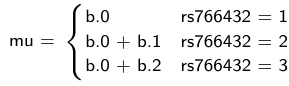](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/hd7image.png) b.1 = the effect of HT vs HM b.2 = the effect of NP vs HM - The hypotheses: 1. H0: b.1 = 0; HM and HT have the same effect 2. H0: b.2 = 0; HM and NP have the same effect ``` model.1 <- "model { for (i in 1:N) { hbf[i] ~ dlnorm(mu[i],tau.t) mu[i] <- b.0+b.1 *equals(rs766432[i],2)+b.2 *equals(rs766432[i],3) } ## prior on precision parameters tau.t ~ dgamma(1,1); ### prior on mean given precision b.0 ~ dnorm(0, 0.001); b.1 ~ dnorm(0, 0.001); b.2 ~ dnorm(0, 0.001); ### prediction lmu.1 <- b.0; hbf.1 ~ dlnorm( lmu.1,tau.t); pred.1 <- step(hbf.1-20) lmu.2 <- b.0+b.1; hbf.2 ~ dlnorm( lmu.2,tau.t); pred.2 <- step(hbf.2-20) lmu.3 <- b.0+b.2; hbf.3 ~ dlnorm( lmu.3,tau.t); pred.3 <- step(hbf.3-20) ### fitted medians by genotypes mu.1 <- exp(lmu.1) mu.2 <- exp(lmu.2) mu.3 <- exp(lmu.3) par.b[1] <- b.0; qpar.b[2] <- b.1; par.b[3] <- b.2 par.h[1] <- hbf.1; par.h[2] <- hbf.2; par.h[3] <- hbf.3; par.m[1] <- mu.1; par.m[2] <- mu.2; par.m[3] <- mu.3 par.p[1] <- pred.1; par.p[2] <- pred.2; par.p[3] <- pred.3 }" data.1 <- source("saudi.data.2.txt")[[1]] model_hbf <- jags.model(textConnection(model.1), data = data.1,n.adapt = 1000) update(model_hbf, 10000) test_hbf <- coda.samples(model_hbf, c("par.b", "par.h", "par.m","par.p"), n.iter = 10000) summary(test_hbf) plot(test_hbf) autocorr.plot(test_hbf) ``` To analyze the convergence we can observe normality in auto-correlation plots. If we wee substantial auto-correlation (lag > X), we can repeat the the MCMC for 100,000 simulations and sample every X steps by using thin = X in coda.samples(); where X is how often order occurs in the plot. test\_hbf <- coda.samples(model\_hbf, c("par.b", "par.h", "par.m","par.p"), n.iter = 1e+05, thin = 30) Depending on which hypothesis we are testing we could also eliminate b.1 or b.2. Or in other situations reparameterizations can reduce correlation. #### ANOVA Example In this example let's consider a study of 5 different treatment groups assigned to wear shirts with differing levels of cotton (15%, 20%, 25%, 30%, and 35%) and strength was measured. We'll code these levels as dummy variables and [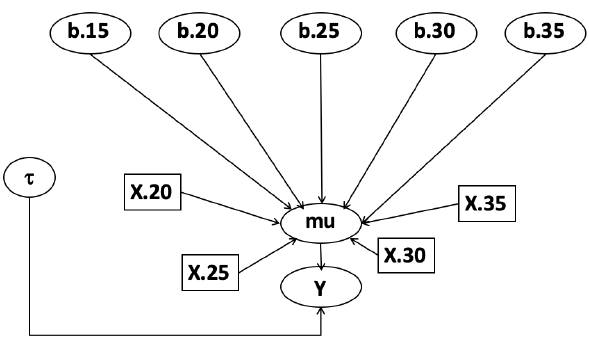](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/jm7image.png) Note that since 15% is the reference group we keep it as a constant. ``` model.1 <- "model { ### data model for(i in 1:N){ y[i] ~dnorm(mu[i], tau) mu[i] <- b.15 + b.20*lev.20[i] +b.25 *lev.25[i] + b.30*lev.30[i] +b.35 * lev.35[i] } ### prior b.15 ~dnorm(0,0.0001); ## referent group b.20 ~dnorm(0,0.0001); b.25 ~dnorm(0,0.0001); b.30 ~dnorm(0,0.0001); b.35 ~dnorm(0,0.0001); tau ~dgamma(1,1) ### difference in strength between level 3 (25%) and level 4 (30%) b.30.25 <- b.30-b.25 ### estimated strength in groups (30%) strength[1] <- b.15 strength[2] <- strength[1]+b.20 strength[3] <- strength[1]+b.25 strength[4] <- strength[1]+b.30 strength[5] <- strength[1]+b.35 }" ``` #### ANCOVA Example These are models that include a continuous covariate and a categorical variable with 2 categories. [](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/TEWimage.png) When the slope differs in the 2 groups and the lines are not parallel [](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/tgYimage.png) ``` model.1 <- "model{ ### data model for(i in 1:N){ hbf_after[i] ~dlnorm(mu[i],tau) Lhbf_baseline[i] <- log(hbf_baseline[i]) mu[i] <- beta.0 + beta.d*Drug[i] + beta.b*(Lhbf_baseline[i]-mean(Lhbf_baseline[])) + beta.i*Drug[i] *(Lhbf_baseline[i]-mean(Lhbf_baseline[])) } ### prior density beta.0 ~ dnorm(0,0.0001) beta.d ~dnorm(0, 0.0001) beta.b ~dnorm(0, 0.0001) beta.i ~dnorm(0,0.0001) tau ~ dgamma(1,1); ### inference parameter[1] <- beta.0 parameter[2] <- beta.d parameter[3] <- beta.b parameter[4] <- beta.i }" ### generate data Drug = rep(0, nrow(hbf.data)) Drug[treatment == "Hy"] <- 1 table(Drug, hbf.data$Drug) data.1 <- list(N = as.numeric(nrow(hbf.data)), hbf_baseline = hbf_baseline, hbf_after = hbf_after, Drug = Drug) model_mean <- jags.model(textConnection(model.1), data = data.1,n.adapt = 1000) update(model_mean, 10000) test_mean <- coda.samples(model_mean, c("parameter"), n.iter = 10000) ``` So if the interaction term is significant then we would conclude the treatment has an effect #### Missing Values Treat missing values in the response as unknown parameters and JAGS will generate them as a form of imputation. Missing data in the covariates however is not so easy. #### Model Selection: DIC - Model selection based on marginal likelihood is most robust but difficult to implement - Often model search over many models is based on BIC using posterior estimates of parameters - Model selection for a small number of models is based on posterior intervals Start from the deviance: -2log(P(y | β, τ )) Deviance information Criterion: DIC = Dbar + pD = Dhat + 2 \* pD Dbar: -2 E(log(P(y | β, τ ))) = posterior mean of the deviance Dhat: -2 log(P(y | β^, τ^ ) = point estimate of the deviance using the posterior means of the parameters pD: Dbar - Dhat = Effective number of parameters The model with the smallest DIC is estimated to be the model that would best predict a replicate dataset of the same structure as the observed. # Hierarchical Models Previously we have assumed given covariates, the observations are independent. However, there are many situations where this does not hold. Bayesian Hierarchical models can be used to cluster observations, where each cluster might have its own cluster-specific parameters. In Bayesian hierarchical models, we start by imposing a prior that is a function of different parameters. We'll introduce a new variable γ, which is called the hyper-prior; The prior of α depends on β, which depends on γ. [](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/J3Rimage.png) Hyper-parameters: Parameters of prior distribution Hyper-Priors: Distribution of Hyper-parameters A typical example of this in medical research is population of hospitals, providers within hospitals, and patients within providers. Any datasets with such a structure are called **hierarchical**. Hierarchical models are also called partial pooled or random effect models. We are interested in making inference of specific units. In doing so observations may be collected over time on the same individuals, so repeated measures must be accounted for. [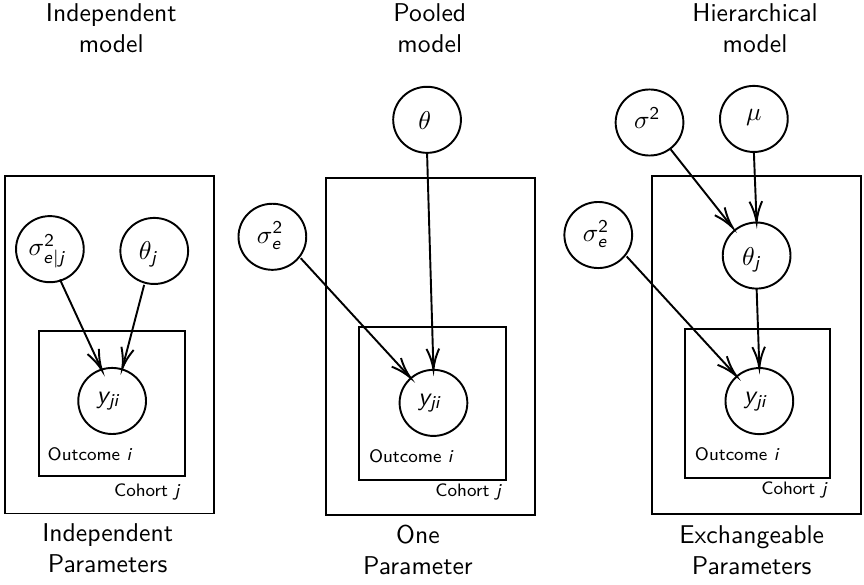](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/fDaimage.png) - Independent models have no randomly-varying effects - Pooled models have a randomly-varying (subject-specific) effects of slope - Hierarchical h ave randomly-varying (subject specific) effects of slope and intercept #### Ranking Posterior Estimates [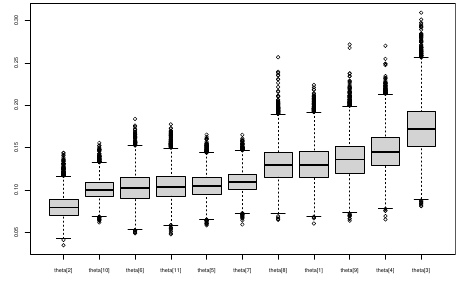](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/Rr2image.png) We can simply rank the outcome/results in a box plot such as the above, but this does not consider the uncertainty of the estimates. We can derive the posterior distribution of each ranking by ranking the estimates at each iteration of the Gibbs Sampling and generate the posterior distributions of the ranks. Below the ranks are in parenthesis: [](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/HFzimage.png) The posterior distribution of ranks gives us a measure of the uncertainty of the ordering. ### Data Formatting There are three main alternative approaches to account for the hierarchical structure of the data in coding, in order of popularity: 1. Nested Indexes - Define an index of the same length of the data that specifies the cluster to which each unit belongs. 2. Offset - Construct a vector of indexes that define the first and last element of each cluster. Needs two indexes Tabular Format: [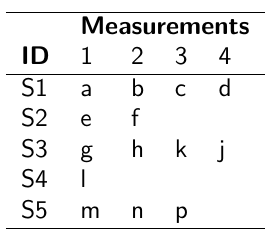](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/srXimage.png) Long Format: [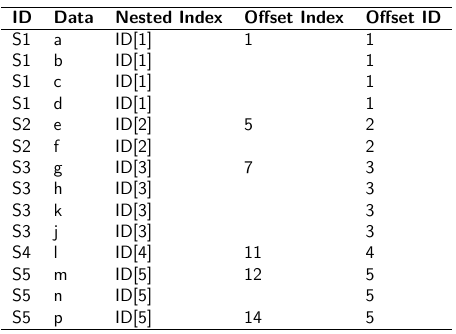](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/NKzimage.png) 3. Data padding - Structure data in array format and fill in empty cells with NA when clusters include different sample sizes ##### Model Implementation With Offset ``` ### Begin by setting up the data and generating the offset ## Prepare outcome and covariate data y <- na.omit(c(t(HB.data[, 6:8]))) # All outcome data y0 <- HB.data[, 5] # Baseline data t <- c(t(HB.data[, c(2, 3, 4)]))[-na.action(y)] # Times corresponding to non-missing outcome ## Fill in data for offset indexes one subject at a time, starting with the first subject i <- 1 offset <- c(1, 1 + length(which(is.na(HB.data[1, 6:8]) == F))) ## Add a new offset for each subject until the end of data while (offset[(i + 1)] < length(y) - 1) { i <- i + 1 offset <- c(offset, offset[i] + length(which(is.na(HB.data[i,6:8]) == F))) # Calculate offsett for subject i } offset <- c(offset, (length(y) + 1)) # Concatenate to the set of offsets model.1 <- "model { for (i in 1:N) { for(j in offset[i] : (offset[i+1]-1)){ y[j] ~ dnorm(psi[j], tau.y) psi[j] <- alpha[i] + beta[i]*(t[j] - tbar) + gamma*(y0[i] - y0bar) } alpha[i] ~ dnorm(mu.alpha, tau.alpha) beta[i] ~ dnorm(mu.beta, tau.beta) } # priors sigma.a <- 1/tau.alpha sigma.b <- 1/tau.beta sigma.y <- 1/tau.y mu.alpha ~ dnorm(0, 0.0001) mu.beta ~ dnorm(0, 0.0001) gamma ~ dnorm(0, 0.0001) tau.alpha ~dgamma(1,1) tau.beta ~dgamma(1,1) tau.y ~dgamma(1,1) y0bar <- mean(y0[]) tbar <- mean(t[]) }" ``` i = subject offset\[i\]: (offset\[i + 1\] -1) = observations corresponding to subject i [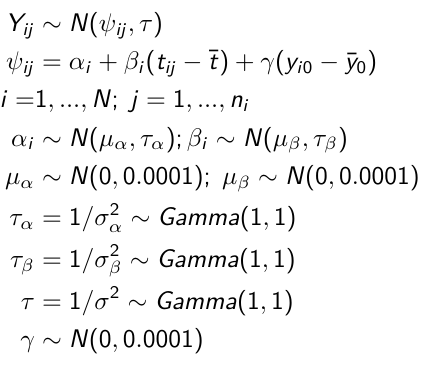](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/22Himage.png) ### Checking Convergence The major assumption of MCMC is convergence. There are 4 widely-used diagnostic plots in R: - Gelman and Rubin: With M >= 2 chains calculate the potential scale reduction factor as ratio of estimated variance of the parameter and within-chain variance - Gewke: Test for equality of means between two non-overlapping parts of the Markov Chain - Raftery and Lewis: Calculates the number of iterations N and the number of burn-ins M necessary for a quantile of interest q to be estimated with an acceptable tolerance r (in (q-r, q+r)) with a probability s - Heidelberg and Welch: Calculates a test statistic to test the null hypothesis that the Markov chain is from a stationary distribution ##### Gelman and Rubin Diagnostics With m chains of length n, GR convergence diagnostic provides numeric convergence summary based on multiple chains (at least 3 chains are required) [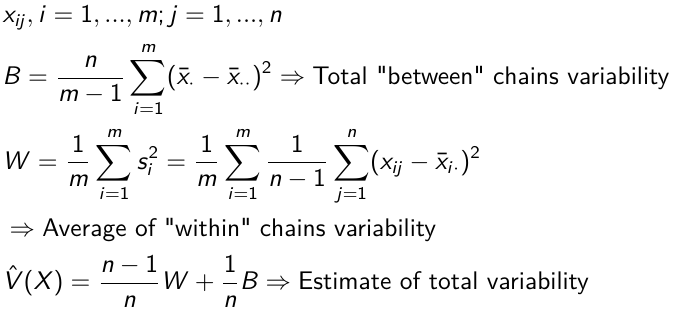](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/cRjimage.png) If the chains are all from stationary distributions: [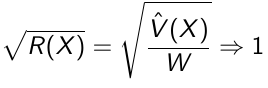](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/7cuimage.png) ``` jags.snp <- jags.model(textConnection(model.snp), data = data.snp, n.adapt = 1500, n.chains = 3) update(jags.snp, 1000) test.snp <- coda.samples(jags.snp, c("beta.snp"), n.iter = 1000) geweke.diag(test.snp, frac1 = 0.1, frac2 = 0.5) gelman.diag(test.snp) gelman.plot(test.snp, ylim = c(1, 4)) ``` [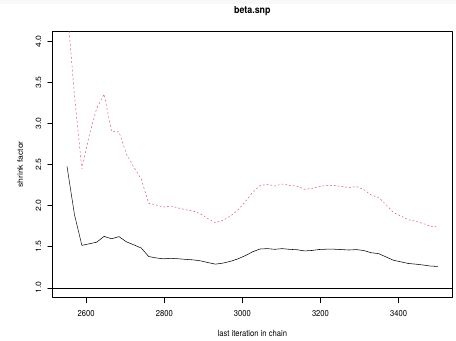](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/VRximage.png) This graph is an example of chains that do not converge; They could be approaching 1 but we see a lot of variability especially near the beginning. [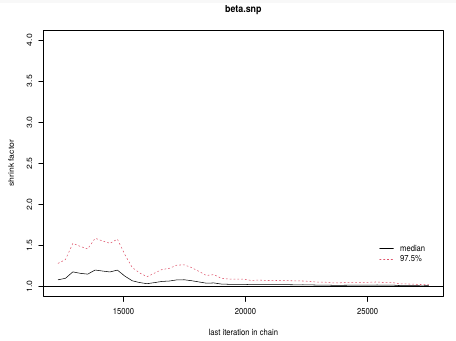](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/mctimage.png) In this plot we can observe the lines converge around 1. ##### Note: Parallel Computing As the number of chains for convergence increases in more complicated models we require more computing power. There are several packages in R that can be used to do this, perhaps the most used being *snowfall* or *doParallel*. ### Comparing Hierarchical Models Joint likelihood of data and parameters: [](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/INaimage.png) There are three primary approaches used: - Deviance Information Criterion (DIC) [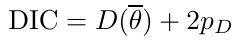](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/hHyimage.png) Which is based on p(y | θ) - Akaike Information Criterion (AIC) AIC = -2 log(y | φ̂) + 2pφ where pφ is the number of hyper-parameters - Bayesian Information Criterion (BIC) BIC = -2 log(y | φ̂) + log(n)\*pφ "Likelihood" is not well defined in a hierarchical model; It depends on the "focus" of the study if we want to use θ, φ, or the model structure without any unknown parameters. It is not a matter of which is correct but which is appropriate for our purpose. Consider an example where our model predicts classes within schools in within a country: - If we are interested in predicting future *classes* in those school then θ is the focus and deviance-based methods such as DIC are appropriate - If we are interested in predicting results of future *schools* in a country then φ is the focus and marginal-likelihood methods such as AIC are appropriate; Relevant to education within the whole country. - If we are interested in predicting results for a new country, then no parameters are in focus, the Bayes factors are appropriate to compare models; Relevant to general statements about education in the - whole world or outside of the country being studied. ## Mixture Models Mixture models integrate multiple data generating processes into a single mode; AKA a mixture of many distributions. This is especially useful in cases where the data doesn't allow us to fully identify which observations belong to which process, such as clustering. [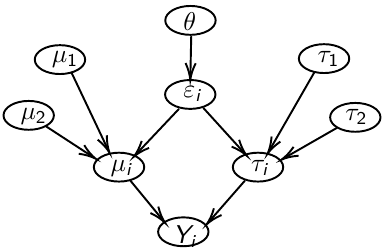](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/86Yimage.png) [](https://bookstack.mitchellhenschel.com/uploads/images/gallery/2023-02/7z5image.png) ``` model.1 <- "model{ p[1] <- theta p[2] <- 1 - theta for( i in 1 : N ) { epsilon[i] ~ dcat(p[]) # dcat: categorical outcome y[i] ~ dnorm(mu[epsilon[i]],tau[epsilon[i]]) } theta ~ dbeta(1,1) for (j in 1:2){ mu[j] ~ dnorm(0.0, .0000001); tau[j] ~ dgamma(1,1) sigma[j] <- pow(tau[j],-2) } }" ``` ε value hidden → two profiles